足し算のはなし
話の流れで前回はコンピュータでの文字表現に進みましたが、順序としては数値の計算のことを簡単に見ておくべきだったかもしれません。なにしろコンピュータは「電子計算機」なのですから、数字を足したり引いたりすることこそ本職です。
*
私たちは買い物をするときでも飲み会の集金をするときでもよく足し算をします。そんなときにいちいち足し算のしくみなど考えもしないと思いますが、ちょっと振り返ってみてください。例えば68+75という2桁の計算です。頭の中では:
*
- 1の位どうしを加える(8+5=13)
- 結果が10以上なので、1の位の結果を3とし、10の位に1を繰り上げる
- 10の位の数と1の位から繰り上がった数を加える(6+7+1=14)
- 再び10以上なので、10の位の結果は4、100の位に1を繰り上げる
- これらの結果、答えは143となる
というような手順を踏んでいるはずです。各桁の結果が10以上になると繰り上がるのは、私たちが10進法を使っていて、一桁の数字は9までしかないからですね。コンピュータの場合は2進数ですから、足した結果が2以上になると桁上がりします。このメカニズムを頭に入れておいてください。
*
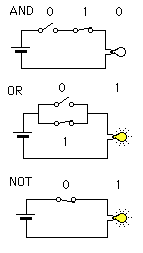 2進数の足し算の前に、ごく簡単な論理演算を見ておくことにします。論理演算なんていうと難しそうですが、A「かつ」Bとか、A「または」Bという条件の組み合わせを調べるあれです。図1のように、電流回路の並列つなぎと直列つなぎを考えると分かりやすいでしょう。直列つなぎの場合、電球が灯るにはA、Bの両方が1(スイッチON)でなければなりません。こういうものをANDと呼びます。並列つなぎを見ると、電球が灯るのは少なくとも片方が1(ON)であればよいことが分かりますね。これはORといいます。もう一つ、普段は電球が灯っていて、スイッチを押したときだけ電気が消えるようなものも考えておきましょう。これはNOTというものです。このAND、OR、NOTがコンピュータの演算の基本になります。どんな複雑な計算も、これらを組み合わせることで成り立っているのです。
2進数の足し算の前に、ごく簡単な論理演算を見ておくことにします。論理演算なんていうと難しそうですが、A「かつ」Bとか、A「または」Bという条件の組み合わせを調べるあれです。図1のように、電流回路の並列つなぎと直列つなぎを考えると分かりやすいでしょう。直列つなぎの場合、電球が灯るにはA、Bの両方が1(スイッチON)でなければなりません。こういうものをANDと呼びます。並列つなぎを見ると、電球が灯るのは少なくとも片方が1(ON)であればよいことが分かりますね。これはORといいます。もう一つ、普段は電球が灯っていて、スイッチを押したときだけ電気が消えるようなものも考えておきましょう。これはNOTというものです。このAND、OR、NOTがコンピュータの演算の基本になります。どんな複雑な計算も、これらを組み合わせることで成り立っているのです。
*
それでは、これらを使って2進数の足し算を行ってみましょう。前に述べたように、足し算にはその桁自身がどうなるかという部分と、繰り上がりがどうなるかという部分がありますから、一桁の足し算のためにこの両者を調べる必要があります。
一番簡単な場合、つまり一桁の2進数をふたつ加える場合の答えのパターンは
| A | B | 桁自身 | 繰上り |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
の4通りです。AとBがどういう関係の時にどんな結果になるか、法則を考えてみてください。
この表を見ると、繰り上がりの方は先ほどの論理演算ANDと同じです。つまり繰り上がりの計算には、直列のスイッチを用意しておけばよいことになります。
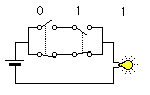 その桁自身の答えはどうでしょう。これは、A,Bの片方が1だった時に1になっています。一見ORのようですが、両方が1の時は0になってしまうので、新しいケースですね。この場合は、少し複雑ですが、図2のように並列の回路に普通のスイッチとNOTスイッチを並べたもので実現できます(これもよくあるケースなので、XORという名前が付けられています)。足し算はこの2組の回路を合わせて実行されるのです。
その桁自身の答えはどうでしょう。これは、A,Bの片方が1だった時に1になっています。一見ORのようですが、両方が1の時は0になってしまうので、新しいケースですね。この場合は、少し複雑ですが、図2のように並列の回路に普通のスイッチとNOTスイッチを並べたもので実現できます(これもよくあるケースなので、XORという名前が付けられています)。足し算はこの2組の回路を合わせて実行されるのです。
2桁以上の足し算は、このような回路を桁数分ずらりと並べて行います。2桁目以上は下の位から繰り上がってきた数も加えなければなりませんから、入力が3つと少し複雑になりますが、基本的には1桁の場合と同じことです。
*
引き算や掛け算なども、論理回路の組み合わせで計算を行うという点では違いありません。乾電池と豆電球とスイッチでこれらの計算回路を作ると随分大きなものになりますが、コンピュータのCPUの中にはこの様な回路が何百万も詰め込まれています。そして高度な科学技術計算も、プログラムの内部ではこういう単純な論理演算の組み合わせに分解され、それらを猛スピードで実行することで複雑な処理を行っているのです。
*
(Beginners' Mac 1996/7号)



